أحجام الأشكال الهندسية

أحجام الأشكال الهندسية: تعتبر الرياضيات من أكثر المواد التي يراها الطلاب صعبة للغاية

ومن غير الممكن النجاح بها إلا أن هذا الأمر خاطئ فهي من أجمل المواد الدراسية والتي تتعلق

بحياتنا بشكل مباشر حيث سنحتاج إلى مفاهيم الرياضيات في الكثير من أعمالنا اليومية المختلفة

وبالتالي لا يجب إعتبارها مادة صعبة ولكن يراها الطلاب هكذا لأنها تعتمد على الفهم بشكل كبير

على عكس الكثير من المواد التي تعتمد على الحفظ، كما تكمن أهمية مادة الرياضيات كونها

تدخل في عدد كبير من التخصصات الجامعية، حيث توجد في المجال الطبي والمجال الهندسي وبعض

مجالات التعليم ولذلك لا يمكن إهمالها أبداً، وإن أكثر ما نجده في تعلم الرياضيات يتعلق بحياتنا اليومية

هي الأشكال الهندسية المختلفة من مثلثات ومربعات ومتوازيات والمكعبات والأسطوانات والدائرة

وغيرها الكثير والتي نجدها في أي مكان من حولنا وبالتالي من الضروري فهم هذه الأشكال

الهندسية وتعلم كيفية حساب مساحاتها واحجامها وكل ما يتعلق بها.

وفي هذا المقال سنتحدث عن أحجام الأشكال الهندسية المختلفة وسنتحدث بشكل خاص

عن الأسطوانة من حيث حجمها وميزاتها وإستخداماتها وغيرها الكثير من المعلومات المهمة،

كما سنعرف لكم معنى الأشكال الهندسية والفوائد منها ولماذا يجب تعلمها وفهمها بشكل جيد.

• ما هي المجسمات أو الأشكال الهندسية:

• إن نظرنا حولنا سنلاحظ وجود الكثير من الأشكال الهندسية حولنا مثل الطاولة والكتاب
• والأقلام والنوافذ والأبواب ومخروط المثلجات وكرة القدم وغيرها الكثير،

حيث تعرف الأشكال الهندسية بأنها عبارة عن أشكال لها ثلاثة أبعاد والتي هي الطول والعرض

والإرتفاع، والتي تساعد بشكل كبير في فهم وتعلم هذه الأشكال المميزة.

• ما هي أنواع المجسمات الهندسية:

يوجد بشكل عام نوعين من المجسمات وذلك تبعاً لشكل السطح وهي المجسمات متعددة السطوح

والمجسمات غير متعددة السطوح:

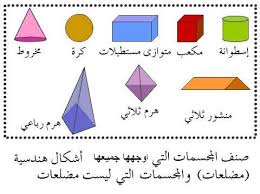
• المجسم متعدد السطوح:

والذي يمكن أن نعرفه بأنه الشكل الهندسي الذي تكون جميع أسطحة مسطحة، ومن الأشكال

الهندسية التي تعتبر مجسمات متعددة السطوح هي المكعب والهرم الثلاثي والمنشور الثلاثي.

• المكعب: وهو عبارة عن شكل هندسي يحوي ستة أوجه مربعة الشكل.
• الهرم الثلاثي: وهو عبارة عن شكل هندسي يضم قاعدة على شكل مثلث وعدة وجوه جانبية على شكل مثلث أيضاً.
• المنشور الثلاثي: وهو عبارة عن شكل هندسي يحوي قاعدتين على شكل مثلث تتواجد على الطرفين والعديد من الوجوه الجانبية مستطيلة الشكل.

• المجسمات غير متعددة السطوح:

وهي عبارة عن الأشكال الهندسية التي تحتوي على سطح واحد على الأقل غير مسطح

ويوجد العديد من الأمثلة عليه مثل الأسطوانة والمخروط والكرة.

• الكرة: وهي عبارة عن شكل هندسي ثلاثي الأبعاد دائري الشكل.
• الأسطوانة: وهي عبارة عن شكل هندسي تتكون من قاعدتين دائريتان ويربط بينهما سطح منحني.
• المخروط: وهو عبارة عن هرم ذو قاعدة مسطحة دائرية الشكل وعدة جوانب مائلة تجتمع مع بعضها في نقطة تسمى رأس المخروط.

• أشهر واكثر المجسمات الهندسية إستخداماً:

• الكرة: من أبرز خصائص هذا الشكل الهندسي هي أن كل نقطة على سطح الكرة تبعد عن المركز مسافة متساوية والتي هي عملياً نصف قطر الدائرة،

كما أن الكرة تتميز بعدم إمتلاكها لأية رؤوس ولها سطح منحن واحد فقط.

يمكن حساب حجم الكرة من خلال القانون كما في الصورة أدناه، حيث أن r هي نصف قطر الكرة.

• المكعب: والذي يحوي على ستة أوجه مربعة الشكل ومتطابقة فيما بينها، كما يضم ثمانية رؤوس والتي تشكل زواياه والتي تنتج من إلتقاء أطراف الحواف معاً،

كما يحوي المكعب على إثنا عشر ضلعاً مستقيماً ومتساوياً في الطول والتي تسمى حواف المكعب وتلتقي وجوه المكعب عند الحواف مع بعضها،

ولمعرفة حجم أي مكعب يتم إستخدام القانون التالي (الطول × العرض × الإرتفاع ) أو القانون التالي (طول الضلع)^3.

• المخروط: يتميز المخروط عن باقي الأشكال الهندسية بانه يحوي على وجه مسطح واحد ولا يحتوي على أية زوايا أو حواف مستقيمة ويوجد نوعين من المخاريط وهي:
• أولاً: المخروط القائم والذي يكون كذلك إذا كان رأس المخروط يقع على إستقامة واحدة مع مركز قاعدته.
• ثانياً: المخروط المائل والذي يكون كذلك إذا كان رأسه لا يقع على إستقامة واحدة مع مركز قاعدته أي انه عكس المخروط القائم.

يتم حساب مساحة المخروط كما يلي: تقسم مساحة المخروط إلى قسمين وهي مساحة قاعدة المخروط والتي هي نفس مساحة الدائرة، والقسم الثاني هو المساحة الجانبية للمخروط.

حيث أن  h هي الطول المائل أو الإرتفاع الجانبي للمخروط، أما حجم المخروط فيحسب من خلال القانون الموضح في الصورة حيث أن h هي ارتفاع المخروط والذي هو العمود الواقع بين رأس المخروط ومركز القاعدة الدائرية و B مساحة القاعدة والتي هي عبارة عن مساحة الدائرة.

• متوازي المستطيلات:

والذي يضم ستة وجوه مستطيلة الشكل، بحيث ان كل وجهين متقابلين متطابقين، ويحوي متوازي المستطيلات على 12 ضلعاً واللذين يمثلون حوافه وعلى ثمانية رؤوس، يتم حساب حجم متوازي المستطيلات من خلال القانون التالي (الطول × العرض × الإرتفاع)، أما المساحة الجانبية لمتوازي المستطيلات فتحسب من خلال القانون (الطول× الإرتفاع × 2+ العرض × الإرتفاع × 2) بينما تحسب المساحة الكلية لمتوازي المستطيلات من خلال القانون التالي (المساحة الجانبية + الطول × العرض × 2).

• المنشور:

وهو شكل ثلاثي الأبعاد يتكون من قاعدتين متطابقتين ومتوازيتين ويختلف شكل قاعدتي المنشور بحسب شكله فقد يكون مربعاً أو مستطيلاً أو خماسياً وحتى سداسياً، ويتم حساب مساحة سطح المنشور وفق العلاقة التالية (مساحة القاعدة × 2) + (محيط القاعدة × ارتفاع المنشور)، أما حجم المنشور فيتم حسابه وفق العلاقة التالية (مساحة القاعدة × الإرتفاع).

• الأسطوانة:

وهي شكل ثلاثي الأبعاد تتكون من قاعدتين دائريتين، وتتميز الإسطوانة بانها لا تحتوي على أية رؤوس أو زوايا، كما انها تحتوي على ثلاثة وجوه وهي الوجه المنحني والحافتين المنحنيتين والقاعدتين الدائريتين.

• يتم حساب مساحة سطح الإسطوانة الكلية وفق العلاقة () والتي تقاس بالوحدات المربعة.
• كما يتم حساب المساحة الجانبية للأسطوانة وفق العلاقة () وتقاس أيضاً بالوحدات المربعة.
• أما حجم الإسطوانة فيتم حسابه وفق العلاقة () والذي يقاس وبالوحدات المكعبة.

• أمثلة تدريبية حول حساب حجم الإسطوانة:

1. لدينا أسطوانة ارتفاعها 10سم ونصف قطر قاعدتها 5سم، أحسب حجم هذه الأسطوانة:

الحل: حجم الإسطوانة= = 10× 3,14× 25= 785

1. لدينا أسطوانة نصف قطرها 4 سم وارتفاعها 10 سم، أحسب حجمها:

الحل: حجم الإسطوانة= = 3,14 × 16 × 10 = 502,4 .

1. لدينا أسطوانة ارتفاعها 12 م وقطرها 8 م، أحسب حجمها:

الحل: حجم الإسطوانة= = 12 × 16 ×3,14 = 602,88 ، وهنا يجب الإنتباه إلى ان المعطى هو القطر وليس نصف القطر وبالتالي نقسم القطر على أثنان للحصول على نصف القطر.

وبهذا نكون قد وصلنا لنهاية مقالنا والذي تحدثنا فيه عن أحجام الأشكال الهندسية و حجم الاسطوانة مع أمثلة عنها.

نتمنى ان ينال إعجابكم

دمتم بخير